This Blog is about Backpropagation.
Contents
1 背景及定义
前向传播以及反向传播是神经网络的基础,前向传播较简单(即按照表达式计算即可),反向传播相对来说较为复杂,本文为在学习了[1]的基础上结合自己的理解所写。
反向传播中最核心的其实就是链式法则(chain rule)(一种用于求解复合函数导数的常用方法,详见[2]),通过其来计算输出相对于输入变量的偏导数(partial derivative)(也就是相对于输入变量的梯度),进而在梯度下降算法中作为梯度来使用。
对每个变量的偏导数告诉我们整个表达式对其值的敏感性。如对于f(x, y) = xy表达式来说,当x = -2,y = 3时,对于x的偏导数为3,表示x增加一个极小值Δ时整个表达式将会减小2Δ倍,同理y增加一个极小值Δ时整个表达式将会增加3Δ倍。
2 一个简单的例子
我们可以将表达式转化为电路(circuit)的形式,这样不仅直观而且便于理解。将表达式:f(x, y, z) = (x + y) z,拆分为q = x + y,f = q × z两个表达式,我们可以将其转换为如下图所示的形式(其中圆圈代表运算符,箭头连接变量与运算符,绿色数字代表正向传播时各变量的值,红色数字代表反向传播时各变量相对于整个表达式的偏导数)。
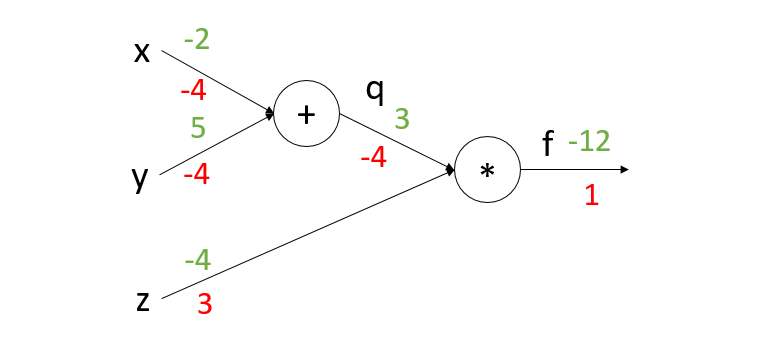
设x = -2,y = 5,z = -4;
前向传播:
q = x + y = -2 + 5 = 3
f = q × z = 3 × -4 = -12
反向传播:
我们所关注的主要是输入对于输出的偏导数,即第2,4,5式。
可以看到,将表达式转换为电路形式后计算前向和反向传播十分直观。链式法则在电路图中的具体体现为:输出对于某一变量(如本例中的x,y,z,q)的偏导数,实际上等于节点”输入和输出“的偏导数的乘积。具体地说如对于本例中的q,将其左边的所有电路都抽象为一个节点,看作输入,对其求偏导数(即偏f/偏q = 偏qz/偏q = z),之后乘以其右边电路已经计算出的偏导数(即偏f/偏f = 1)(如下图所示)。
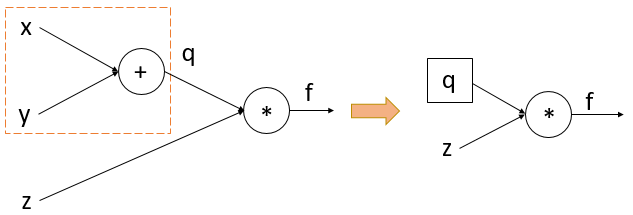
这样做的好处是:我们只需要计算每个节点的偏导数(即输入输出乘积),而不需要去关心整个表达式。这样,无论多么复杂的表达式只要拆分合理,都可以对其轻松求导。就好像反向传播中的“传播”二字一样,在电路中进行偏导数值的传播。
注:2,3式之所以多乘了一个“偏f/偏f”是为了便于说明以上观点。
3 一点小技巧
3.1 电路压缩
在实际应用中,转化电路不一定要每一个运算符都拆分。当已知整体表达式中部分表达式偏导数形式时,可以对电路图进行“压缩”,这样便于计算。
比如:在逻辑回归算法中,sigmod函数我们已知其导数为如下公式,所以我们可以将这一部分进行压缩。
对于如下逻辑回归表达式:
压缩前后的对比如下图所示:
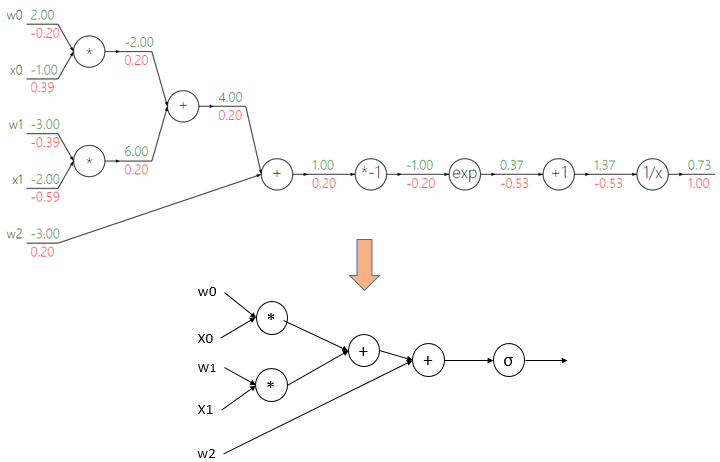
可以看到,我们直接用一个节点代替了sigmod运算中的四个节点,从而压缩了模型,提高了计算的效率。
3.2 常用电路
其实在电路拆解中,最常用的节点无非就是加节点和乘节点。
-
加节点所做的就是将输出的偏导数原封不动的传递给其所有子节点。如第一节中的电路:对于x+y,x的偏导数 = y的偏导数 = 输出的偏导数 = -4。
-
乘节点所做的就是将将两子节点的值互换再乘以输出的偏导数。如第一节中的电路:对于q × z,q的偏导数 = z的值 × 输出的偏导数 = -4 × 1 = -4,z的偏导数 = q的值 × 输出的偏导数 = 3 × 1 = 3。
4 复杂一点呢
下面我们来计算一个复杂的例子:
转化为电路后如下图所示(前向传播的值已经给出):
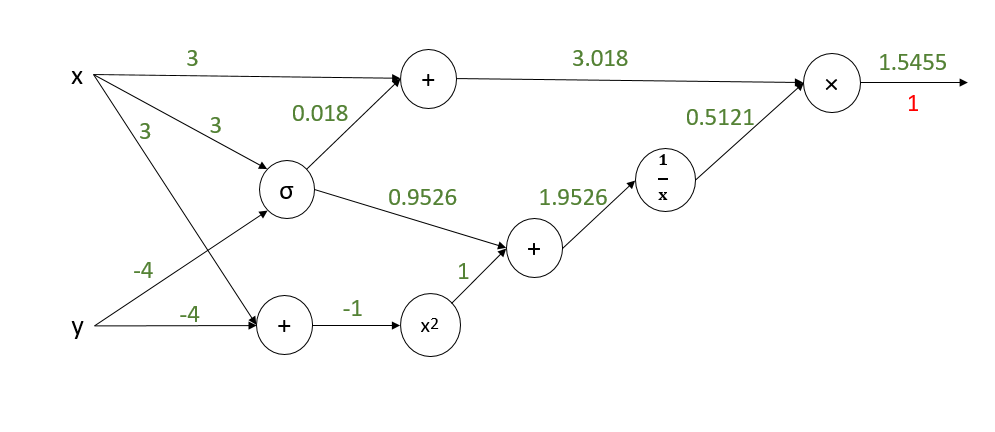
开始反向传播:
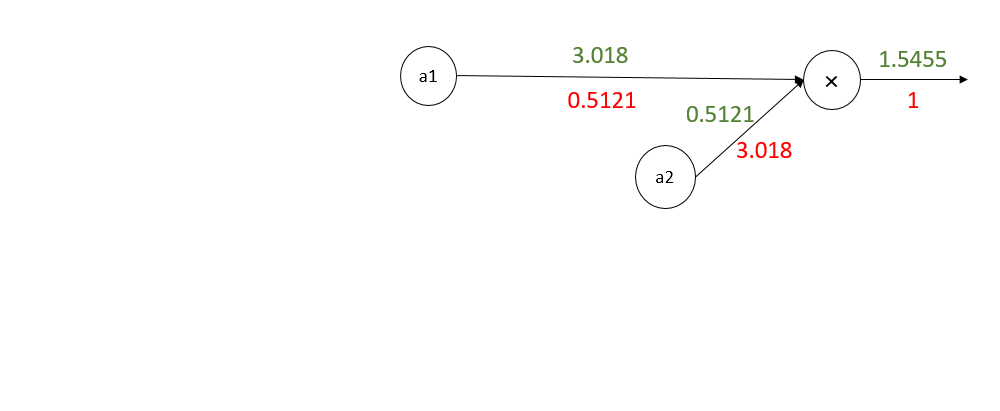
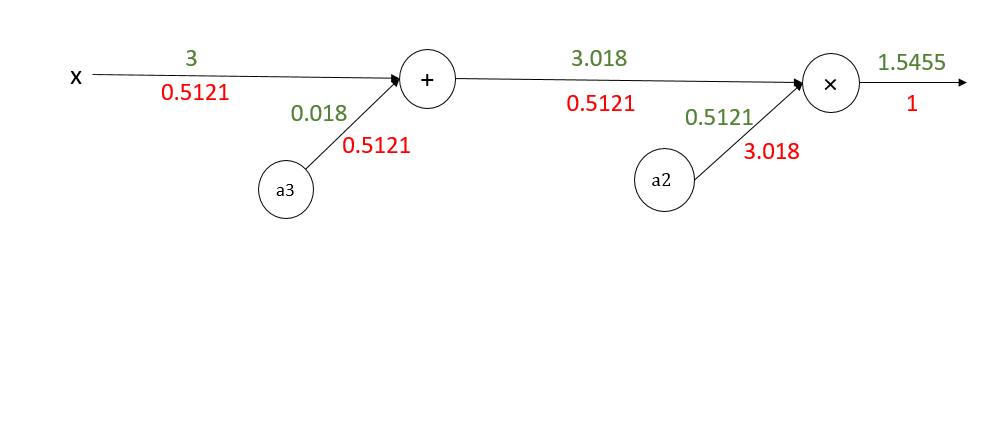
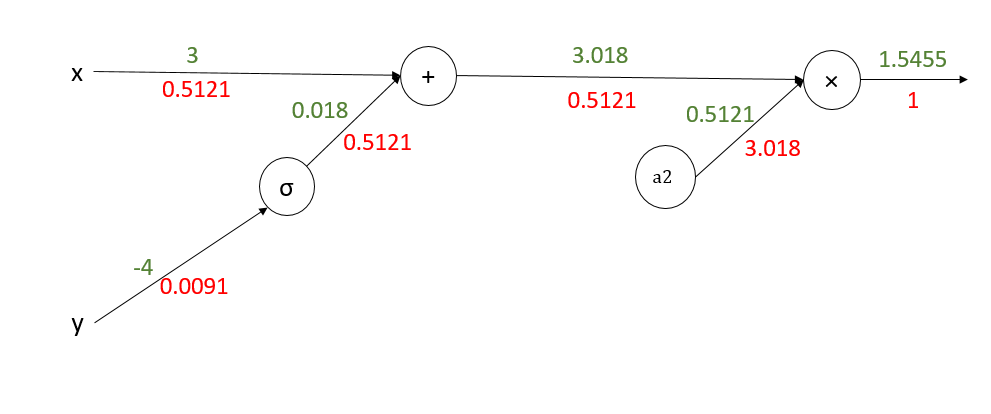
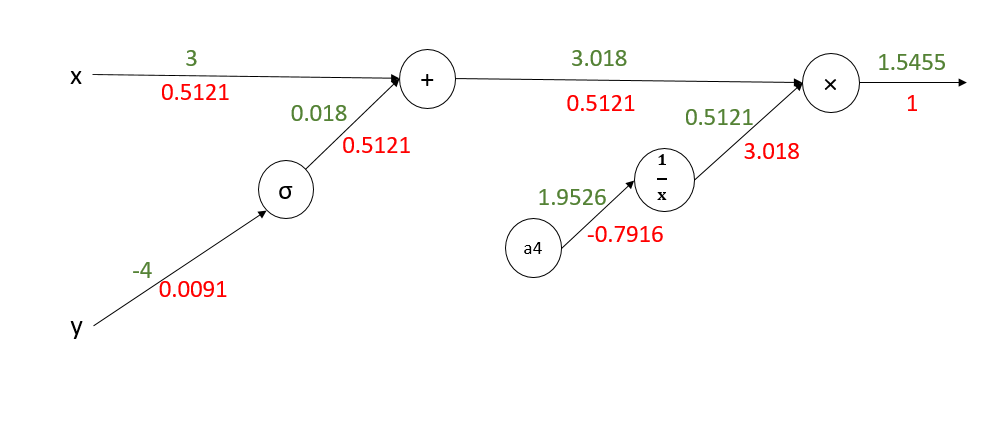
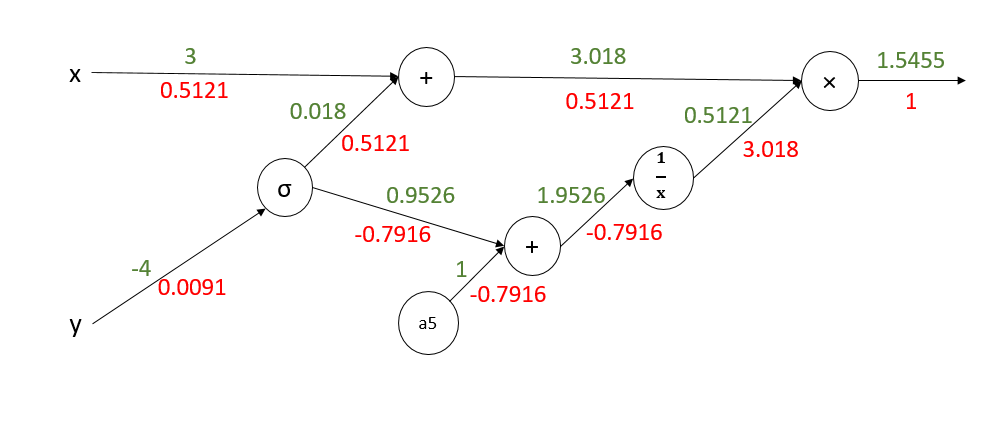
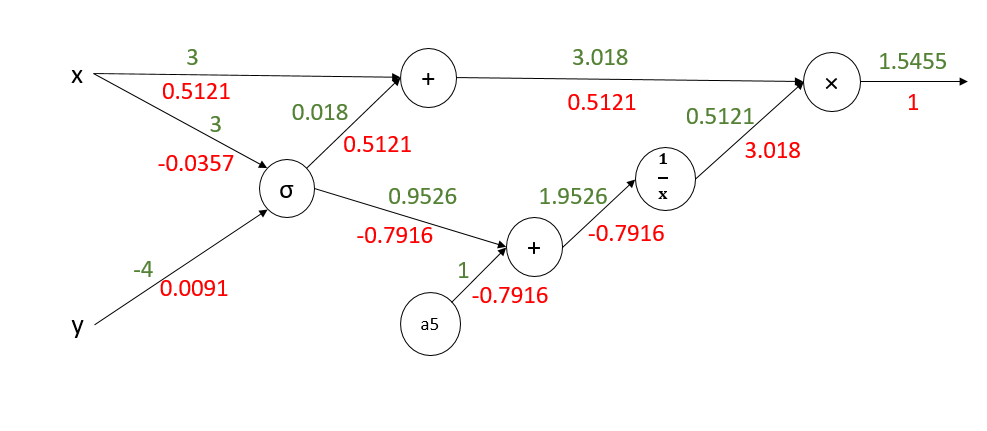
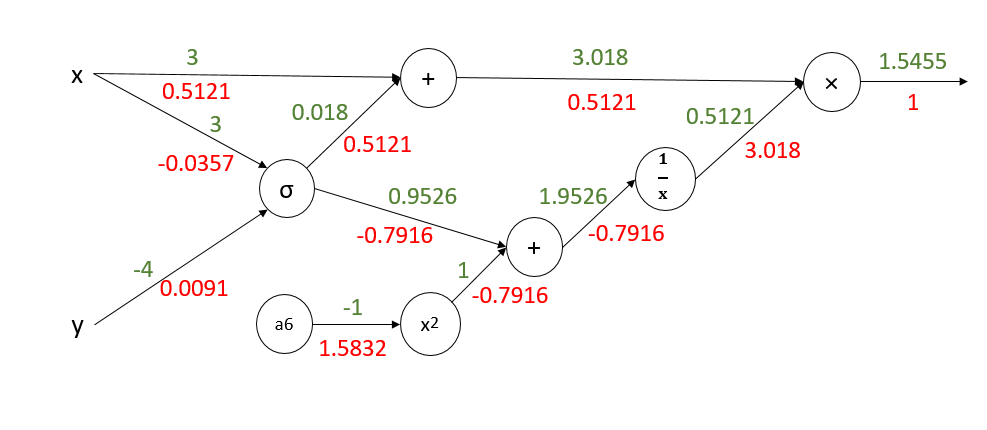
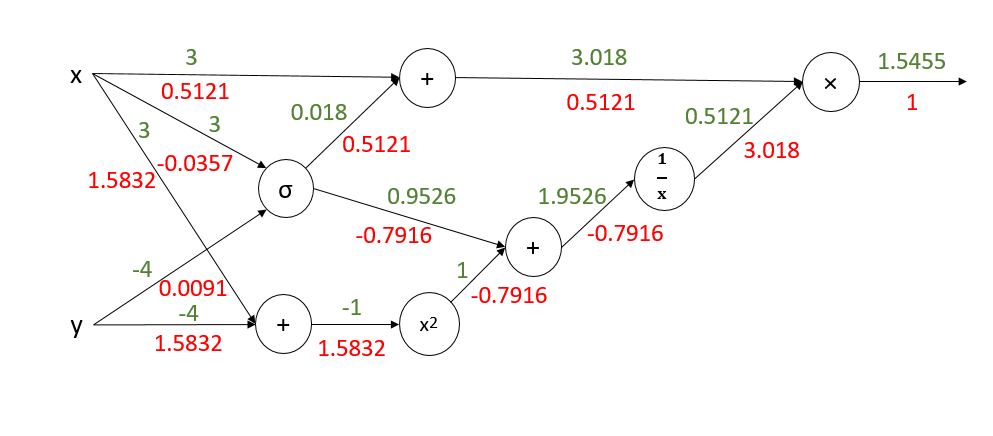
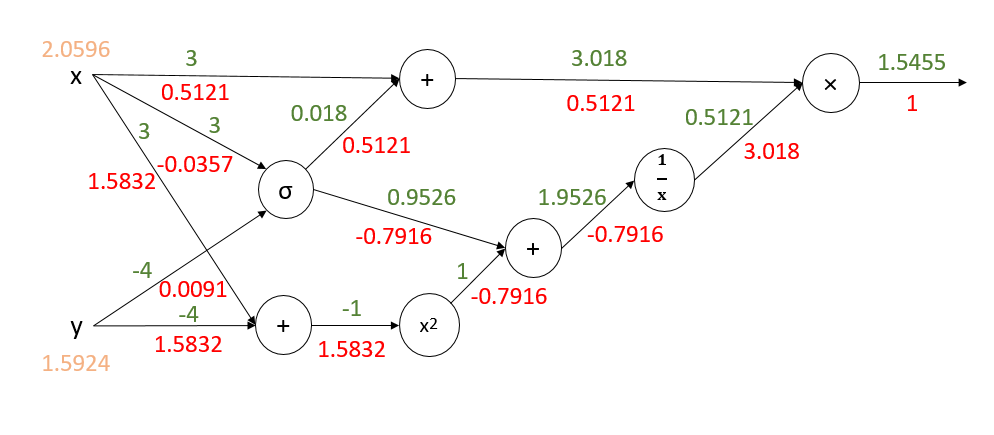
注:x,y的偏导数是所有分支偏导数的加和。